Quick: What's wrong with this photo?

It's winter time. Let's talk about snowflakes.
Doing it all wrong
Did you ever make paper snowflakes in elementary school?
If so, you probably made them like the picture above. (Or maybe the picture below, if you had a really adventurous teacher.)

You were also probably told that no two snowflakes are alike, and you imagined a myriad array of possibilities. You were also, surely, led to believe that snowflakes are symmetric (with symmetries governed by the dihedral group Dn for some n).
But all of that is bogus, and has been known to be so since 1611!(*) Perhaps the most annoying thing is that the truth is more exciting than this fiction... Kepler's paper, "A New Year's Gift, or, On the Six-Cornered Snowflake," is widely considered the origin of the sphere-packing problem that has piqued mathematicians' and grocers' interests alike for hundreds of years. Anyhow, the facts are:
- the only possible symmetries are n = 3, 6, 9, 12, ..., with n = 6 accounting for the lion's share;
- the likelihood that a naturally occurring snowflake is actually (6-fold) symmetric is ZERO;
- snowflakes are far from unique, indeed every snowflake begins as a hexagonal disc, and remains so for quite awhile;
- the imagined myriad array is, in fact, only a 5 x 7 table of possibilities.
The truth is more physics than mathematics, but, as a "symmetry" in nature, it is one of the many things you might learn about in Giaquinto's HONR 204 course. You might also try the 2001 book by the estimable British mathematician Ian Stewart.
How to do it right
It's not too hard to fold paper in a way that will give you 6-fold symmetry. Here's one tutorial.
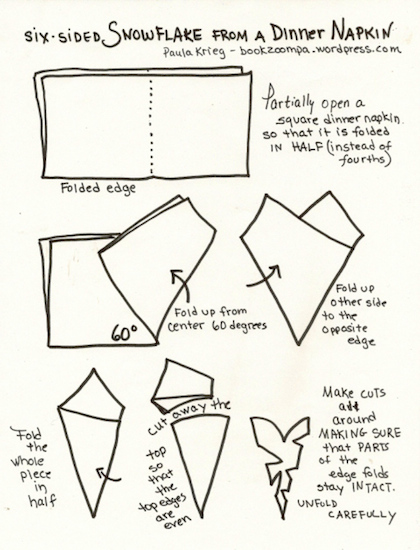
(Final quiz: what happens if you skip the last fold depicted at bottom-left above?)
And here's Vi Heart to take us out.
